Ole Peters |
Home | Publications | Research | |

|
Economics Convection My work in this field has led me to question the foundations of the current economic formalism. I propose to re-derive neo-classical economics from an improved basis. To follow this project, visit our blog or follow me on twitter. For a non-technical introduction there's also a TEDx talk. | |||
The problem with the foundations
| Economics uses a model of human decision-making that seems fundamentally flawed to me. At the very core and beginning (1650s) of quantitative economic theory lies the assumption that humans optimize expectation values of monetary wealth. This turns out to be a poor model of real observed human behavior, as everyone agrees. In my opinion, the community has come to a set of conclusions that are correct but also a dead-end. Currently common responses to the failure of the economic null-model of human behavior are: 1) Humans perceive money (somewhat) non-linearly. 2) Humans perceive probabilities (somewhat) non-linearly. 3) Humans are (somewhat) irrational. 4) Humans do not (fully) optimize. 5) Humans are not (primarily) interested in wealth. They all have something in common: they are all negations and strictly speaking they are all trivially true. Linearity, rationality, and optimality are all idealizations and correspond to mathematical concepts that cannot be borne out perfectly in reality. And modeling humans as creatures that are solely interested in wealth accumulation leaves out what makes life worthwhile. However, to a reasonable approximation, of course humans do perceive money and probabilities linearly, are rational, optimize, and prefer more cash in the bank to less. In a first step I'm happy to accept and work with these approximations. From my perspective, responses 1-5 hint at a more fundamental flaw, and I propose a different conclusion. I take issue with a notion that is not even a reasonable approximation: the formalism posits that the object that is being optimized in the human decision process is mathematically well represented by an expectation value. A priori there is no reason to believe this. | The correction
| My interpretation of the failure of the economic null-model is not only a negation. It suggests an alternative: there are good reasons to believe that the object that is being optimized in the minds of men is one that is well represented by time-average changes in a mathematical model of wealth dynamics. This statement requires some explanation. Firstly, some economics texts claim that expectation values are considered because they reflect long-time behavior (e.g. Chernoff and Moses (1959): "If a game is `favorable' from the point of view of the expectation value and you have the choice of repeating it many times, then it is wise to do so. For eventually, your amount of money [is] bound to increase.") This is incorrect in general, i.e. it is not correct that expectation values reflect long-time behavior. It is the case for ergodic observables, but for example the position of a simple random walk is not ergodic: the time-average of a random-walk position is known as the "random acceleration process", and it does not converge to anything. It just wanders off -- the average wanders off, not just the position itself. An important model of wealth dynamics, the null model for all of mathematical finance and the reason why we read about GDP growth in the newspaper as a percentage change over the previous year, is geometric Brownian motion -- a very general form of multiplicative growth. This model is not ergodic either, and this introduces a difference between time-average behavior and expectation values (something we've certainly known since Kiyosi Ito's famous 1944 paper). 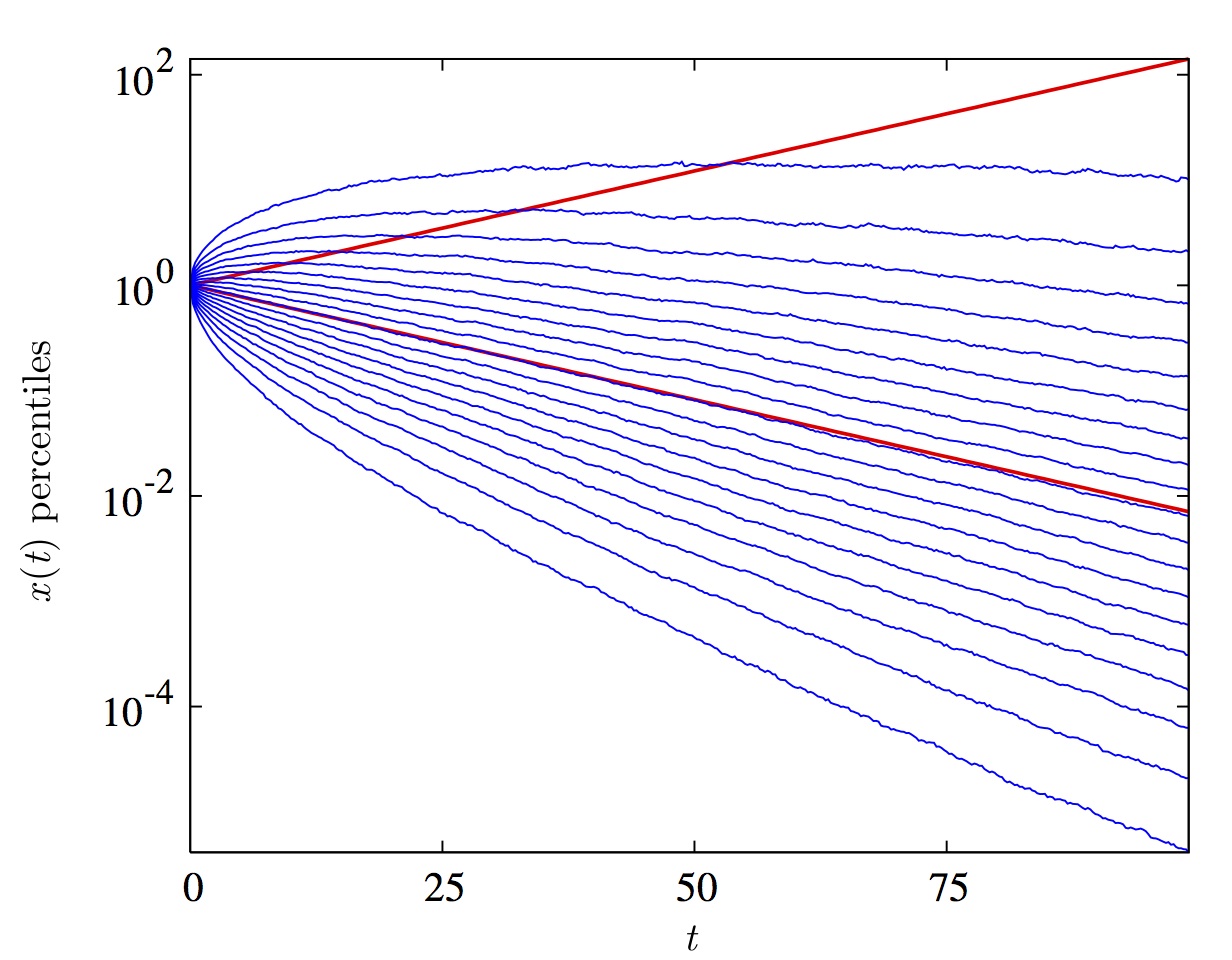
Figure 1: Illustration from Peters and Klein (2013), using geometric Brownian motion with drift term 0.05 per time unit and squared noise amplitude 0.2 per time unit. The up-sloping red line is the expectation value as a function of time, the down-sloping line has the time-average slope. Blue lines are quantiles as a function of time, from top (95% quantile) to bottom (5% quantile) in steps of 5%. The expectation value does not reflect what happens over time. The possibility of a difference between expectation values and time averages was not known when we formulated the economics model of human behavior in the 17th and 18th centuries. Only in the mid-19th century, when physics imported concepts of randomness that had originated in economics did it become clear that ergodicity can fail (the term "ergodicity" was coined by Boltzmann in 1884). Expectation values, from a modern perspective, are averages over imagined parallel universes. "Parallel universes" are a mathematical trick -- figments of the imagination -- that can simplify computations, but (in this context) they are not real in the specific sense that by definition we cannot communicate with parallel universes. Therefore, the findings of any theory must not depend on what happens in a parallel universe (the techniques may at intermediate steps involve such concepts, but the findings must not depend on their assumed existence). Our economic theories cavalierly violate this principle. Does the change in approach I propose matter? Yes. It matters because I propose to change our concept of rationality. All of the currently prevailing economic formalism has to be re-derived from this modern starting point. With my collaborators I have begun this work, see publications. | ||
|
|