
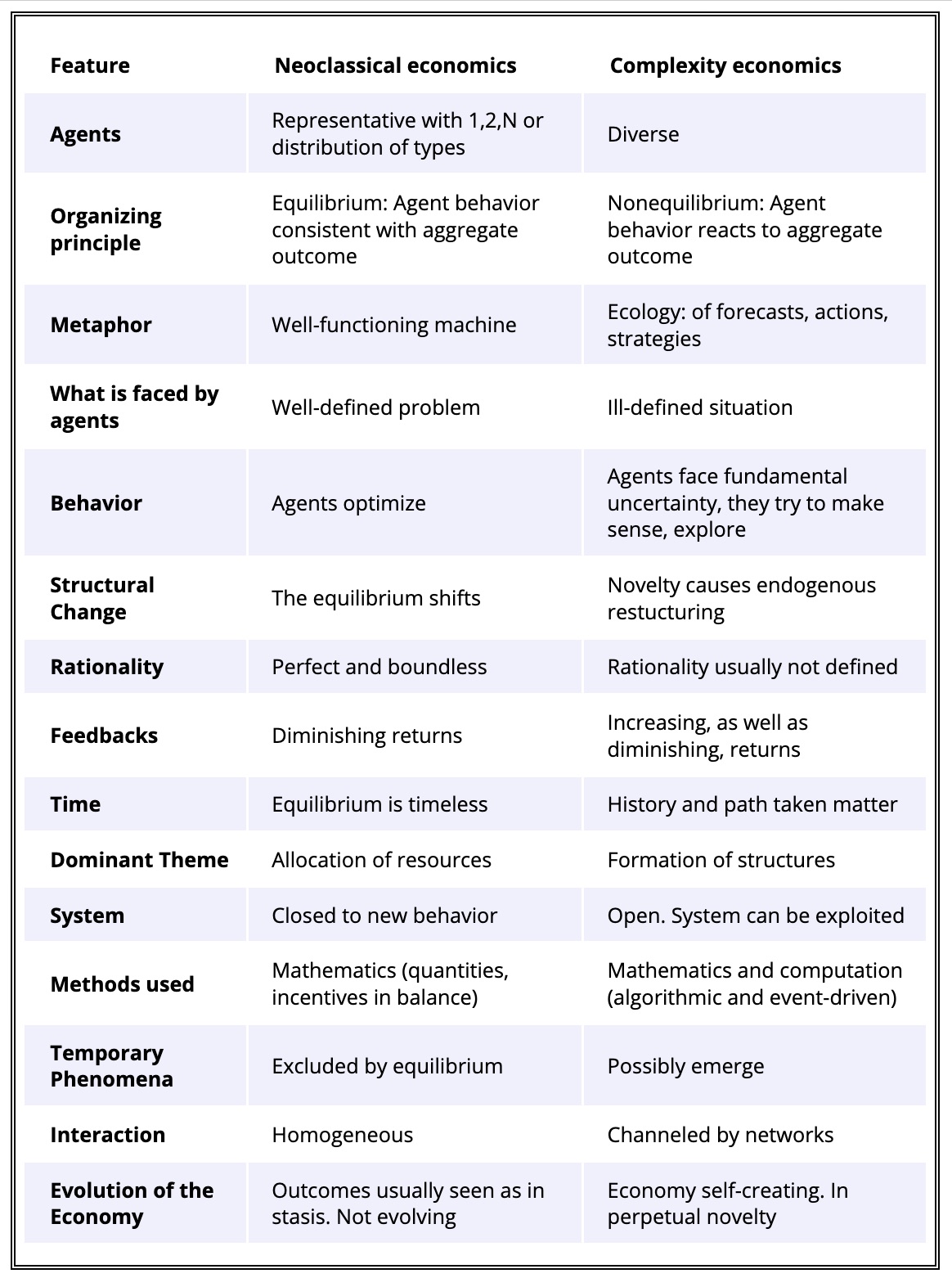
Complexity Economics
Economics in the last few years has generated a number of new approaches. One of these—complexity economics—was pioneered in the 1980s and 1990s by a small team at the Santa Fe Institute led by W. Brian Arthur. The standard framework sees behavior in the economy as in an equilibrium steady state. People in the economy face well-defined problems and use perfect deductive reasoning to base their actions on. The complexity framework by contrast sees the economy as always in process, always changing. People try to make sense of the situations they face using whatever reasoning they have at hand, and together create outcomes they must individually react to anew. The resulting economy is not a well-ordered machine, but a complex evolving system that is imperfect and perpetually constructing itself anew.
The new approach is not just an extension of standard economics, nor does it consist of adding agent-based behavior to standard models. It gives a different, nonequilibrium view of the economy: one where actions and strategies constantly evolve, where time becomes important, where structures constantly form and re-form, where phenomena appear that are not visible to standard equilibrium analysis. This view gives us a world closer to that of political economy than to neoclassical theory, a world that is organic, evolutionary and historically-contingent.
Here is a table of differences between standard economics and complexity economics.
An example: The El Farol Bar Problem
Book: Complexity and the Economy
W. Brian Arthur, Oxford Univ. Press, 2015
The book is a collection of Arthur's papers on complexity and the economy.
The papers cover a range of topics: the El Farol problem, the artifical stock market, competing technologies and lock-in, how economic systems are gamed, cognition in the economy, how complexity evolves in systems, how the economy forms from its technologies, how technology evolves, among others.
Preface to the book: Complexity and the Economy
Some Q & A about Complexity Economics (printable pdf version)
Question: Is there a logical basis for the complexity view?
Arthur: There is. Complexity economics is based on the proposition that the economy is not necessarily in equilibrium. Economic agents (firms, consumers, investors) constantly change their actions and strategies in response to the outcome they mutually create. This further changes the outcome, which requires them to react anew. Agents therefore live in a world where their beliefs, actions, and strategies are constantly being tested for survival within an outcome or "ecology" these beliefs, actions and strategies mutually create. Sometimes the system will settle to an equilibrium, sometimes it may not: it might show perpetually novel behavior, or new phenomena that don't appear in steady state.
Often we can model such systems using analytical tools: nonlinear dynamics, or nonlinear stochastic process theory. Often we must resort to computational experiments—we compute outcomes and study how these form.
Q. How does this relate to "complexity"?
A. Complex systems are ones with multiple elements adapting or reacting to the pattern these elements create. The elements might be individual cars reacting to cars in front or behind them, to the "traffic" patterns they form. In complexity, individual elements adapt to the world—the aggregate pattern—they co-create. With the economy, agents—whether they are banks, consumers, firms, or investors,—continually adjust their market moves, buying decisions, prices, and forecasts to the situation these moves or decisions or prices or forecasts together create. So complexity is a natural way to look at the economy. In a way this viewpoint isn't new. Adam Smith pointed out that aggregate patterns form from individual behavior and individual behavior responds to those aggregate patterns. This is really an economics of things coming into being and it focuses on patterns forming, structures changing, and the consequences of permanent disruption.
Q. How does this approach fit with standard economics?
A. In complexity economics we ask how agents react to the aggregate pattern they create. That's the natural question, but it's complicated. So to seek analytical solutions, economics historically asked instead what agents’ behavior might be consistent with the aggregate pattern it creates—would be in equilibrium with the outcome it creates. General equilibrium theory asks: What prices and quantities of goods produced and consumed are consistent with—would pose no incentives for change to—the overall pattern of prices and quantities in the economy’s markets? Classical game theory asks: What strategies, moves, or allocations are consistent with—would be the best course of action for an agent (under some criterion)—given the strategies, moves, allocations his rivals might choose? Complexity economics by contrast asks how actions, strategies, or expectations might endogenously change with the patterns they create. It is a nonequilibrium approach.
Q. So complexity economics and nonequilibrium economics are closely related?
A. They are. In fact, I'd prefer to think of nonequilibrium economics. I cooked up the label "complexity economics" when I did a piece on this for Science in 1999. The editor asked me to name this approach and so I called it "complexity economics." I regret this slightly. Nonequilibrium emphasizes disruption — the constant disruption that comes from agents adjusting to a situation that's always changing. Complexity emphasizes agents reacting to changes that other agents make. The two concepts are closely related.
Q. Complexity and uncertainty are related too, aren't they?
A. Yes. In the complexity approach, you can't assume that all problems that agents face are well defined. This is because agents simply don't know how other agents might react. They don't know how others see the same problem. Therefore there is real Knightian uncertainty. This means that agents need to cognitively structure their problems — the have to "make sense" of them, as much as solve them. So this brings us into the world of cognition, and of behavioral economics.
Q. Isn't much of this approach based on simulation? So how can we take it seriously?
A. There is indeed a lot of agent-based computation used in the approach. But I don't like to think of this as "simulation." The object is not to reproduce or "simulate" reality. It is to study the consequences of some particular world, some assumed model of part of the economy. Sometimes you can do this with conventional mathematics. But sometimes you have to compute the outcomes. So I prefer to think of this as doing carefully controlled computer experiments. If done rigorously, you can link particular assumptions to the outcomes they create. Standard theoretical economics does this with the "naked mind." But if things get complicated, say the agents differ, we have to resort to computation—a sort of telescope for the naked mind. There's plenty of scope for sloppy work here, but the same can be said for conventional analysis. There's also plenty of scope for rigorous exploration of patterns and the causes behind them. Exploratory computational mathematics proceeds this way; it can uncover much and it can be done well or poorly. Computational experiment as a rigorous lab tool is an art form, and it's used in all the sciences.
Q. How does complexity economics fit with agent-based computational economics? Are these approaches related?
A. Yes, they are. In the 1980s computation arrived in economics, and this more than anything else allowed economic theorists to venture beyond the standard neoclassical assumptions. For instance, we could allow complicated inductive reasoning and compute its consequences. If you turn these new possibilities into a theoretical framework you get complexity economics, or something like it. If you turn them into a solution method you get agent-based computational economics. There's no fixed boundary between the two approaches. You could then regard agent-based computational economics as a key method within the framework of complexity economics; or you could regard complexity economics as a conceptual foundation behind agent-based economic modeling. The two approaches are not the same: complexity economics emphasizes emphasizes theory, and agent-based computational economics emphasizes computational technicalities. But overall, I'm happy to say, the two approaches blend together. Depending on whether a study emphasizes theory or method, it can fly either flag—or both.
Q. How did you get into this area?
A. Throughout the 1980s I'd been working on increasing returns economics — now very much a branch of complexity. I was at Stanford, and in 1987 Kenneth Arrow invited me to the Santa Fe Institute, then just starting. I was brought back a year later to direct a research program on "The Economy as an Evolving Complex System." This turned out to be SFI's first research program. We began to ask: what would it be like to do economics out of equilibrium? I had excellent people: David Lane, probability theorist; Richard Palmer, physicist; Stu Kauffman, theoretical biologist; John Holland, computer scientist. Frank Hahn, Arrow, and Tom Sargent were visitors. Out of that a lot of work came. There have been many others outside SFI involved of course, and I'd like to mention in particular Peter Allen, Rob Axtell, Eric Beinhocker, Richard Bronk, Josh Epstein, Doyne Farmer, Andy Haldane, Alan Kirman, Kristian Lindgren, and Leigh Tesfatsion. Now this approach is thriving and younger people are coming along. But the Santa Fe group was the first coherent effort in this area, and laid down much of the approach.
Q. Doesn't this nonequilibrium and complexity view go back a long way in economics?
A. There's indeed a long history of this line of thinking in economics. Many of the themes we are exploring — innovation, disruption, deciding under fundamental uncertainty — occur in Schumpeter, Veblen, Hayek, Shackle, and others. They aren't exactly new in economics. What's changed is that we can now investigate them rigorously. We have much better tools at our disposal, including much more sophisticated probablity theory and the possibility of doing carefully controlled computer experiments.
Q. You have talked about two great problems in economics. What are they?
A. One is allocation within the economy: how quantities of goods and services and their prices are determined within and across markets. This is represented by the great theories of general equilibrium, international trade, and classical game theory. The other is formation within the economy: how an economy emerges in the first place, and grows and changes structurally over time. This is represented by ideas about innovation, economic development, structural change, and the role of history, institutions, and governance in the economy. The allocation problem is well understood and highly mathematized, the formation one less well understood and barely mathematized. Complexity economics looks at structures forming in the economy, so it's just as much concerned with formation as with allocation.
Q. Isn't all this controversial?
A. No, not any more. Complexity economics is an extension of equilibrium economics to the nonequilibrium case. And since nonequilibrium contains equilibrium it's a widening of economics — a generalization. So that's not controversial, that's inevitable. It's really the beginning of a lot of work to be done.
Q. If it's as important as you say, why are we not seeing more of complexity economics in standard departments?
A. Well, we are seeing quite a bit. But it takes about a generation or more for any science to change. Rob Axtell is fond of pointing out that game theory took about 40 to 50 years to fully make its way into economics. And behavioral economics which got started in the 1960s is only now fully arriving. By that measure complexity economics still has a good 10 or 20 years to go. The compensation is that it's fun to work on a field that's opening up, and I think this form of economics is only beginning.
Q. You've said that complexity economics is inevitable. Why?
A. It's not a matter of fashion, or a temporary fad. All the sciences are changing from looking at the world as highly ordered, mechanical, predictable, and in some sort of stasis; to looking at it as evolving, organic, not predictable, and in perpetual discovery. Physics, chemistry, mathematics, geology — they've all moved this way. Economics will too, it may be slightly behind but it always tracks the Zeitgeist.
Q. Is there a killer app for complexity economics? Something that can't be done without it?
A. I can think of two. One is the increasing-returns work done in the 1980s that shows how network effects lead to lock-in and dominance of one or a few players. This can't be done by equilibrium economics — it's not an equilibrium phenomenon. Now all of Silicon Valley accepts this theory and operates by it.
The other killer app is asset pricing. Complexity doesn't assume there is a (rational-expectations) equilibrium and set out to find it. It assumes investors don't know what the market is doing and must learn for themselves what works — which itself changes the market. The results show phenomena seen in real markets: technical trading, correlations among price and volume, and periods of high volatility followed by low volatility (GARCH behavior). The theory explains real world financial phenomena.

